4 Preliminares y notación

4.1 Conjuntos y espacios vectoriales

En la formulación de redes logísticas humanitarias, las decisiones suelen representarse en espacios euclidianos de dimensión finita. Dos subconjuntos relevantes son:

$\mathbb{R}^n$: espacio vectorial real de dimensión $n$.
$\mathbb{R}_{+}^n = \{x \in \mathbb{R}^n : x_i \geq 0,\ \forall i\}$: ortante no negativo, usado para modelar flujos, inventarios o asignaciones no negativas.

Estos conjuntos garantizan que las variables del modelo respeten restricciones físicas (por ejemplo, no es posible enviar una cantidad negativa de ayuda humanitaria).

4.2 Convexidad y conjuntos especiales

La estructura geométrica del espacio factible influye directamente en la complejidad del problema. En particular:

Conjunto convexo: $C \subseteq \mathbb{R}^n$ es convexo si para todo $x, y \in C$ y $\lambda \in [0,1]$, se cumple $\lambda x + (1-\lambda)y \in C$. En logística, la convexidad permite combinar estrategias factibles sin violar restricciones. Sin embargo, la presencia de decisiones binarias (como abrir o no un almacén) rompe esta propiedad, como se discute en el Capítulo 3.
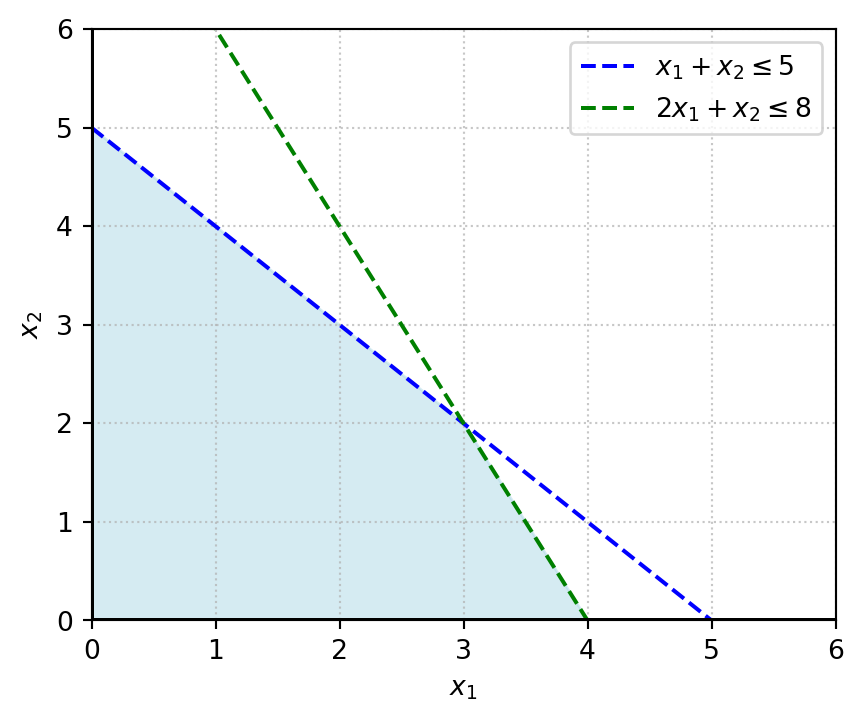
Poliedro convexo: conjunto de la forma $\{x \in \mathbb{R}^n : Ax \leq b\}$ con $A \in \mathbb{R}^{m \times n}$, $b \in \mathbb{R}^m$. Es cerrado y convexo (Bazaraa et al., 2013), y describe sistemas de restricciones lineales como límites de capacidad o cobertura de demanda.

Región factible convexa en el primer cuadrante, acotada por dos líneas rectas y los ejes coordenados, con área sombreada que representa combinaciones factibles de flujos o niveles de inventario. — Figura 4.1: Representación gráfica de un poliedro convexo en $\mathbb{R}^2$, definido por el sistema de desigualdades lineales $x_1 + x_2 \leq 5$, $2x_1 + x_2 \leq 8$, $x_1 \geq 0$, $x_2 \geq 0$. La región factible, sombreada en azul claro, corresponde al conjunto de soluciones admisibles para un subproblema de asignación de inventario o flujo en un modelo de localización–inventario. Su estructura poliédrica refleja la linealidad de las restricciones de capacidad, cobertura de demanda y no negatividad, y garantiza convexidad cuando las decisiones de apertura de almacenes están fijas.

Conjunto cerrado en dimensión finita: En $\mathbb{R}^n$ con la topología euclidiana, un conjunto es cerrado si contiene todos sus puntos límite. Todo subespacio vectorial de $\mathbb{R}^n$ es cerrado, y en dimensión finita, los conjuntos cerrados y acotados son compactos (teorema de Heine–Borel). Esta propiedad es clave para garantizar existencia de soluciones en optimización.

4.3 Funciones y propiedades analíticas

La formulación del costo total en inventario humanitario depende de propiedades analíticas que facilitan el análisis de optimalidad:

Función convexa: $f: \mathbb{R}^n \to \mathbb{R}$ es convexa si
\[ f(\lambda x + (1-\lambda)y) \leq \lambda f(x) + (1-\lambda)f(y), \quad \forall x,y, \lambda \in [0,1]. \] La convexidad garantiza que todo mínimo local sea global, una propiedad deseable en diseño de redes.
Función estrictamente cuadrática: $f(x) = \tfrac{1}{2} x^\top Q x - b^\top x + c$, con $Q \in \mathbb{R}^{n \times n}$ simétrica. Si $Q$ es constante, el Hessiano $\nabla^2 f(x) = Q$ también lo es, lo que simplifica el análisis de curvatura en modelos de costo.
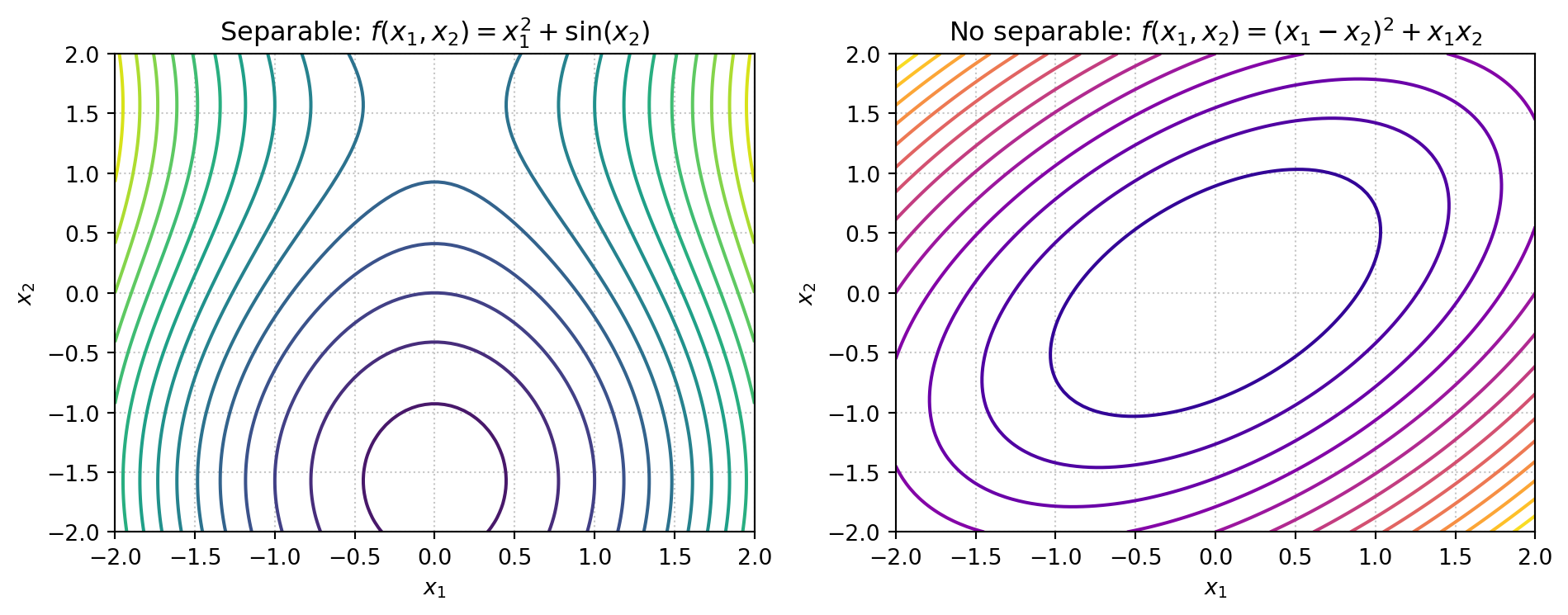
Separabilidad: $f(x)$ es separable si puede escribirse como $f(x) = \sum_{i=1}^n f_i(x_i)$. Esta propiedad permite descomponer el problema en subproblemas independientes, útil en redes con nodos débilmente acoplados. La función de costo no es separable, debido a la interacción entre tamaño de lote, inventario de seguridad y penalización por faltantes.

Dos gráficos de contorno en $\mathbb{R}^2$: el primero muestra líneas de nivel verticales y horizontales (separable); el segundo muestra líneas inclinadas diagonalmente (no separable), ilustrando el acoplamiento entre variables de decisión. — Figura 4.2: Comparación entre una función separable y una no separable mediante curvas de nivel. A la izquierda, $f(x_1,x_2) = x_1^2 + \sin(x_2)$ es separable, pues su estructura no acopla las variables: las curvas de nivel son alineadas con los ejes, lo que permite optimización por coordenadas. A la derecha, $f(x_1,x_2) = (x_1 - x_2)^2 + x_1 x_2$ es no separable, con curvas inclinadas que reflejan interacción entre decisiones una característica clave en modelos de inventario humanitario, donde el tamaño del lote, el inventario de seguridad y la penalización por faltantes están fuertemente acoplados.

4.4 Notación de orden matricial

$A \succ 0$: matriz simétrica $A$ es definida positiva, es decir, $x^\top A x > 0$ para todo $x \neq 0$. Esta notación es útil al analizar la curvatura de funciones cuadráticas en modelos de inventario.

4.5 Formulaciones de optimización mixta

La integración de decisiones estratégicas (ubicación) y tácticas (inventario) da lugar a formulaciones mixtas:

Formulación big-M estándar: restricción de la forma $y \leq M x$, con $x \in \{0,1\}$, $y \in \mathbb{R}_+$, y $M > 0$ suficientemente grande, usada para modelar la implicación lógica $x = 0 \Rightarrow y = 0$. Por ejemplo, si no se abre un almacén ($x = 0$), no puede enviar ayuda ($y = 0$).

4.6 Teoría de probabilidad, incertidumbre y medida de Lebesgue

En contextos humanitarios, la demanda es incierta. Para modelarla rigurosamente, es necesario entender que la medida de Lebesgue generaliza el concepto de “volumen” y permite integrar funciones más allá del cálculo clásico. Esto sustenta la definición de variables aleatorias absolutamente continuas, aquellas cuya probabilidad se expresa mediante una densidad.

Variable aleatoria (v.a.) absolutamente continua: $\mathbb{P}(X \in A) = \int_A f_X(x)\,dx$, donde $f_X$ es la densidad respecto a la medida de Lebesgue. Esta formulación es esencial para modelar demandas con distribuciones suaves, como la normal.
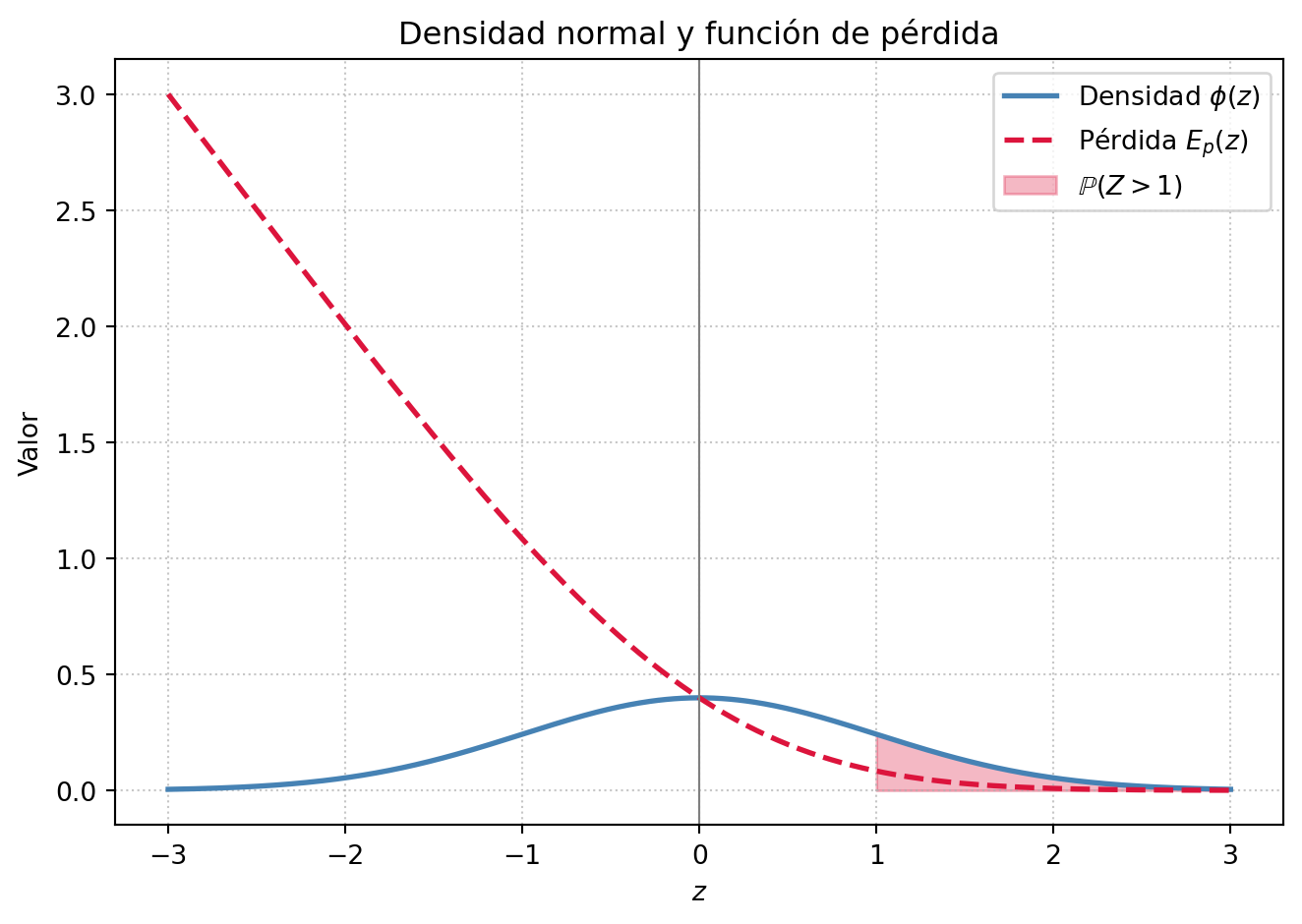
Distribución normal: si $D_L \sim \mathcal{N}(\mu_L, \sigma_L^2)$, su densidad es
\[ \phi_{D_L}(d) = \frac{1}{\sqrt{2\pi}\sigma_L} \exp\!\left(-\frac{(d - \mu_L)^2}{2\sigma_L^2}\right). \] Esta distribución se usa para aproximar la demanda durante el tiempo de entrega, lo que permite calcular el inventario de seguridad.
Varianza: para una v.a. $\tilde{X}$, $\operatorname{Var}(\tilde{X}) = \mathbb{E}[(\tilde{X} - \mathbb{E}[\tilde{X}])^2]$. La varianza cuantifica la incertidumbre en la demanda; ignorarla (por ejemplo, al usar solo $\mathbb{E}[d_j]$) puede inducir soluciones frágiles en eventos extremos.

Gráfica con dos curvas: una en azul sólido (densidad normal) y otra en rojo punteado (función de pérdida convexa), con área sombreada en la cola derecha que representa la probabilidad de eventos extremos. — Figura 4.3: Función de densidad de probabilidad $\phi(z)$ y función de pérdida logística $E_p(z) = z(\Phi(z)-1) + \phi(z)$ asociadas a la distribución normal estándar. La densidad $\phi(z)$ (azul sólido) modela la incertidumbre en la demanda estandarizada, mientras que la función de pérdida $E_p(z)$ (rojo punteado) cuantifica el déficit esperado normalizado cuando el nivel de inventario es insuficiente ($z < 0$). La región sombreada para $z \geq 1$ ilustra la probabilidad de cola superior, relevante para el cálculo del inventario de seguridad en contextos humanitarios. Esta función es fundamental para internalizar el riesgo de faltantes en la formulación del costo total.

Notación $\ll$: indica que una cantidad es mucho menor que otra. Por ejemplo, en la Sección 3.4.4 se muestra que, si se ignora la incertidumbre en $L$, la varianza estimada puede ser $80 \ll 10\,080$, subestimando severamente el riesgo.

El valor esperado $\mathbb{E}[d_j]$ representa la demanda media en la localidad $j$. Aunque es común usarlo como estimador puntual en modelos deterministas, como se advierte en la Sección 3.1.2.3, esta simplificación puede ser inadecuada en logística humanitaria, donde la cola de la distribución (eventos extremos) es crítica.

4.7 Optimización y condiciones de optimalidad

Condiciones de Karush–Kuhn–Tucker (KKT): condiciones necesarias de optimalidad local bajo restricciones de desigualdad y calificación de restricciones. Como se expone en Lewis y Overton (2013), estas condiciones no garantizan optimalidad global en problemas no convexos, como el propuesto, donde la no convexidad surge de las variables binarias y la no linealidad en la incertidumbre.